Question

Consider the equation below. (if an answer does not exist, enter dne.) f(x) = 5 sin(x) + 5 cos(x), 0 ? x ? 2? (a) find the interval on which f is decreasing. (enter your answer using interval notation.)

Answer 1

Answer:
`\bold{[(\pi)/(4),(5\pi)/(4)]}`

Explanation:

Step 1: Create a table

x | 5sinx + 5cosx = y

0 | 0 + 5 = 5

`(\pi)/(2)` | 5 + 0 = 5

π | 0 + -5 = -5

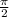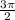`(3\pi)/(2)` | -5 + 0 = -5

2π | 0 + 5 = 5

Notice that y = 5 at 0 and
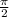`(\pi)/(2)` , so there will be a vertex at their midpoint. Similarly at y = -5.

Midpoint of 0 and
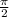`(\pi)/(2)` is
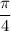`(\pi)/(4)` . Midpoint of π and
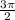`(3\pi)/(2)` is
`(5\pi)/(4)`

(graph is attached to confirm interval)