Answer:
The solution of the equation is y = 1/3
Explanation:
The given equation is 27·y³ - 27·y² + 9·y - 1 = 0
The equation can be solved by plotting using Microsoft Excel or an online tool
To solve the cubic equation, we can use the trial by error method and check for factors;
First we try (y - 1) as a factor, and check if the equation is correct for y = 1, from which we have;
f(1) = 27·1³ - 27·1² + 9·1 - 1 = 8 ≠ 0
We note that the equation is of the form (3·y)³ + 3³·y² + 3²·y - 1 = 0, and from the plot using Microsoft Excel, a solution is at x = 0.
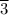(which is the result arrive at using Wolfram Alpha), therefore, we can try (3·y - 1) = 0, from which we have, x = 1/3
f(1/3) = 27·(1/3)³ - 27·(1/3)² + 9·(1/3) - 1 = 27/27 - 27/9 + 9/3 - 1 = 1 - 3 + 3 - 1 = 0
Therefore, (3·y - 1) is a factor of the equation
We divide the given equation by (3·y - 1), to get;
(27·y³ - 27·y² + 9·y - 1)/(3·y - 1) = 9·y² - 6·y + 1
27·y³ - 9·y²
-18·y² + 9·y - 1
-18·y² + 6·y
3·y - 1
Therefore, we have;
(27·y³ - 27·y² + 9·y - 1) = (3·y - 1) × (9·y² - 6·y + 1)
The factor, 9·y² - 6·y + 1, can be written as (3·y)² - 2·(3·y) + 1, which we can write as (3·y)² - 2·(3·y) + 1 = (3·y - 1)², therefore, we have;
(27·y³ - 27·y² + 9·y - 1) = (3·y - 1) × (9·y² - 6·y + 1) = (3·y - 1) × (3·y - 1)² = (3·y - 1)³
∴ 27·y³ - 27·y² + 9·y - 1 = (3·y - 1)³ = 0, therefore, 3·y = 1 is the equation's solution from which we can write the solution of the equation as y = 1/3.