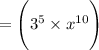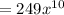Question

How do you simplify expressions with rational exponents

Answer 1

Explanation:

Simplify expression with rational exponents can look like a huge thing when you first see them with those fractions sitting up there in the exponent but let's remember our properties for dealing with exponents. We can apply those with fractions as well.

Examples

(a)
`(p^4)^{(3)/(2)}`

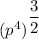
From above, we have a power to a power, so, we can think of multiplying the exponents.

i.e.

`(p^{^ {(4)/(1)}})^{(3)/(2)}`

`(p^{^ {(12)/(2)}})`

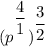
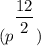
Let's recall that when we are dealing with exponents that are fractions, we can simplify them just like normal fractions.

SO;

`(p^{^ {(12)/(2)}})`

`= (p^( 6))`

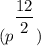
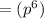
Let's take a look at another example

`\Bigg (27x^{^\Big{6}} \Bigg) ^{{(5)/(3)}}`

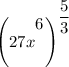
Here, we apply the
`(5)/(3)` to both 27 and
`x^6`

`= \Bigg (27^{{(5)/(3)}} * x^\Big{(6)/(1)* {{(5)/(3)}} }\Bigg)`

`= \Bigg (27^{{(5)/(3)}} * x^\Big{(2)/(1)* {{(5)/(1)}} }\Bigg)`

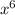
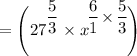
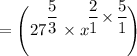
Let us recall that in the rational exponent, the denominator is the root and the numerator is the exponent of such a particular number.

∴

`= \Bigg (\sqrt[3]{27}^(5) * x^(10) }\Bigg)`

`= \Bigg (3^(5) * x^(10) }\Bigg)`

`= 249x^(10)`