Question

1.2.

Prove the following the trigonometric identity step-by-step
1.2.1 sin theta/sin theta+cos theta=tan theta/1+tan theta​

Answer 1

The identity is proved below.

Explanation:

The tangent of an angle
`\theta` is given by:

`tan(\theta) = (sin(\theta))/(cos(\theta))`

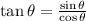
In this question, we are given the following trigonometric identity:

`(sin(\theta))/(sin(\theta)+cos(\theta)) = (tan(\theta))/(1+tan(\theta))`

Applying the tangent

`(sin(\theta))/(sin(\theta)+cos(\theta)) = ((sin(\theta))/(cos(\theta)))/(1+(sin(\theta))/(cos(\theta)))`

Now, we apply the least common multiple on the denominator. So

`(sin(\theta))/(sin(\theta)+cos(\theta)) = ((sin(\theta))/(cos(\theta)))/((cos(\theta)+sin(\theta))/(cos(\theta)))`

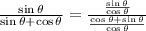
SImplifying the cosine:

`(sin(\theta))/(sin(\theta)+cos(\theta)) = (sin(\theta))/(sin(\theta)+cos(\theta))`

Which means that the identity is proved.