Question

(adapted from Ross, 2.31) Three countries (the Land of Fire, the Land of Wind, and the Land of Earth) each make a 3 person team. Each team consists of three ninjas, each of a different rank: one genin junior ninja, one journeyman ninja, and one elite ninja.

(a) If a ninja is chosen at random from each of the three different countries, what is the probability of selecting a complete team? (A complete team here is a group consisting of three ninjas, each ninja of a different rank).

(b) If a ninja is chosen at random from each of the three different countries, what is the probability that all 3 ninjas selected have the same rank?

Answer 1

Answer: ITS 2 WEEKS AGO IT DOSE T MATTER IF IM RIGHT OR NOT HEHHEHEJSSHAGAGAHAHHAHAA

Explanation:

Answer 2

The answer is "
`(2)/(9) \ and \ (1)/(9)`"

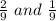Explanation:

In point a:

The requires 1 genin, 1 chunin , and 1 jonin to shape a complete team but we all recognize that each nation's team is comprised of 1 genin, 1 chunin, and 1 jonin.

They can now pick 1 genin from a certain matter of national with the value:

`\frac{1}{\binom{3}{1}}=(1)/(3) .`

They can pick 1 Chunin form of the matter of national with the value:

`\frac{1}{\binom{3}{1}}=(1)/(3) .`

They have the option to pick 1 join from of the country team with such a probability:
`\frac{1}{\binom{3}{1}}=(1)/(3)`

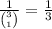
And we can make the country teams:
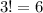`3! = 6` different forms. Its chances of choosing a team full in the process described also are:

`6 * (1)/(3)* (1)/(3)* (1)/(3)=(2)/(9).`

In point b:

In this scenario, one of the 3 professional sides can either choose 3 genins or 3 chunines or 3 joniners. So, that we can form three groups that contain the same ninjas (either 3 genin or 3 chunin or 3 jonin).

Its likelihood that even a specific nation team ninja would be chosen is now:
`\frac{1}{\binom{3}{1}}=(1)/(3)`

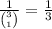
Its odds of choosing the same rank ninja in such a different country team are:
`\frac{1}{\binom{3}{1}}=(1)/(3)`

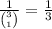
The likelihood of choosing the same level Ninja from the residual matter of national is:
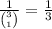`\frac{1}{\binom{3}{1}}=(1)/(3)` Therefore, all 3 selected ninjas are likely the same grade:
`3* (1)/(3)* (1)/(3)* (1)/(3)=(1)/(9)`