Question

How do I solve this?

Answer 1

Consider the point P where the gears meet. When the smaller gear rotates clockwise, the larger one will rotate counterclockwise.

Through one rotation of the smaller gear, P will have traveled the circumference of the smaller gear, which is
`8\pi` in.

At the same time, a point P' on the larger gear traverses the same distance along the larger gear's circumference. This point traces out an arc that is subtended by some angle
`\theta`. The arc is as long as the smaller gear's circumference.

The measure of a circle's interior angle subtended by an arc is proportional to a complete revolution, i.e. an angular displacement of
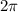`2\pi` radians:

`\frac{14\pi\,\mathrm{in}}{2\pi\,\mathrm{rad}}=\frac{8\pi\,\mathrm{in}}\theta\implies\theta=\frac{8\pi}7\,\mathrm{rad}\approx205.7^\circ`

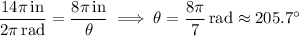
For part 2, we apply the same reasoning to the larger gear. In one full rotation of the larger gear, the point P' traverses the circumference
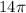`14\pi` in, and so does the point P on the smaller gear.

`\frac{8\pi\,\mathrm{in}}{2\pi\,\mathrm{rad}}=\frac{14\pi\,\mathrm{in}}\theta\implies\theta=\frac{7\pi}2\,\mathrm{rad}=630^\circ`

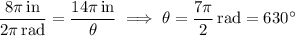
A full rotation is 360 degrees, so the smaller gear would have rotated
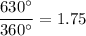`(630^\circ)/(360^\circ)=1.75` times.