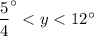Let
 be the length of the leg with one tick mark and
be the length of the leg with one tick mark and
 the length of the leg with two tick marks.
the length of the leg with two tick marks.
In the upper triangle, the law of cosines says
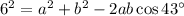
In the lower triangle, it says
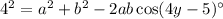
Subtract the second equation from the first to eliminate
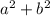 :
:
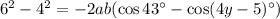
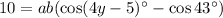
 and
and
 are lengths so they must both be positive. 10 is also positive, so in order to preserve the sign on both sides of this equation, we must have
are lengths so they must both be positive. 10 is also positive, so in order to preserve the sign on both sides of this equation, we must have


Now we have to be a bit careful. If
 is an acute angle, then as
is an acute angle, then as
 gets larger, the value of
gets larger, the value of
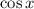 gets smaller. So if we have two angles
gets smaller. So if we have two angles
 and
and
 , with
, with
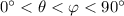 , then we would have
, then we would have
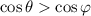 .
.
This means in our inequality, taking the inverse cosine of both sides would reverse the inequality:
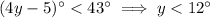
We know that
 is an angle in a triangle, so it must be some positive measure:
is an angle in a triangle, so it must be some positive measure:
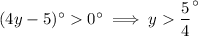
So we must have