Question

Answers for 7 & 8 , conditional probabilities- geometry module 6 version 2

Answer 1

7) I'm assuming any pizza comes with cheese by default and that it shouldn't technically count as a topping on its own. It's probably safe to also assume that a pizza with sausage and pepperoni, for instance, is the same as a pizza with pepperoni and sausage, i.e. the order of toppings does not matter.

Then the number of pizzas that can be made with no more than 5 toppings would be

`\displaystyle\sum_(t=0)^5(12!)/(t!(12-t)!)=1586`

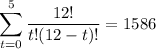
8) Let
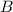`B` be the random variable representing the earning/loss after drawing a bead.
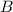`B` has the probability mass function

`p(B=b)=\begin{cases}\frac3{12}=\frac14&\text{for }b=3\\\\\frac7{12}&\text{for }b=-1\\\\\frac2{12}=\frac16&\text{for }b=10\\\\0&\text{otherwise}\end{cases}`

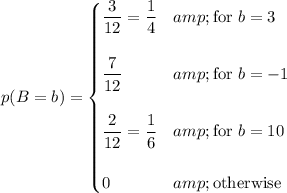
The expected value for any given draw is

`E[B]=\displaystyle\sum_{b\in\{3,-1,10\}}b\cdot p(B=b)=\frac34-\frac7{12}+\frac{10}6=\frac{11}6`

The game would be fair if the expectation was $0, but this one is actually in favor of the player.