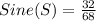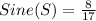Question

What is the trigonometric ratio for sin S ?

Express your answer, as a simplified fraction.

Answer 1

`QR=√(68^2-60^2)\\QR=√(4624-3600)\\QR=√(1024)\\QR=32\\\\sinS=(32)/(68)\\sinS=(8)/(17)`

Answer 2

For this case, we have that by definition:

Be a rectangular triangle and an "x" angle.

`Sine (x) = \frac {CO} {H}`

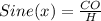
CO is the leg opposite the angle and H the hypotenuse

We want to find the Sine (S) according to the figure shown:

`Sine {S} = \frac {QR} {68}`

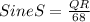
We do not have the opposite leg, we must apply the Pythagorean theorem, which states:

`H = \sqrt {(CO) ^ 2 + (CA) ^ 2}`

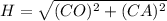
Where:

H: Hypotenuse

CO: Opposite leg

CA: Adjacent leg

In this case, we must find CO:

`CO = \sqrt {H ^ 2- (CA) ^ 2}`

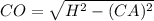
Where:

`H = 68\\CA = 60`

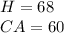
Substituting:

`CO = \sqrt {68 ^ 2-60 ^ 2}\\CO = \sqrt {4624-3600}\\CO = \sqrt {1024}\\CO = 32`

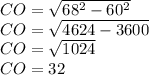
So, we have:

`Sine (S) = \frac {32} {68}`

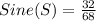
Answer:

`Sine (S) = \frac {32} {68}`

`Sine (S) = \frac {8} {17}`