Answer:
The measure of
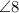 is 60°
is 60°
 and
and
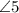 are corresponding angles.
are corresponding angles.
Explanation:
Given that,
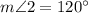
In the given diagram,
 and
and
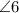 are corresponding angles and their measures are same.
are corresponding angles and their measures are same.
So,
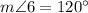
Now,
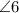 and
and
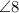 are pair of linear angles.
are pair of linear angles.
That means......
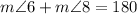 °
°
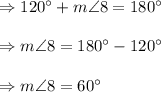
So, the measure of
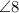 is 60°
is 60°
The type of angles for
 and
and
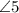 is corresponding.
is corresponding.