Question

What is the area of a parallelogram ABCD

Answer 1

Area of a parallelogram would be 13.46

Explanation:

Since area of a parallelogram is represented by the formula

Area =
`(1)/(2)` (
`(D_(1)*D_(2))`

Where
`D_(1)` and
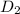`D_(2)` are two diagonals of the given parallelograms.

In the given figure
`D_(1)=AC` and
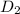`D_(2)` = BD

We will find the length of
`D_(1)` and
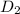`D_(2)` first

Since points A and C are (3,6) and (5,1)

So distance AC =
`\sqrt{(6-1)^(2)+(3-5)^(2)  }`

=
`\sqrt{5^(2)+(-2)^(2)}`

=
`√(25+4)=√(29)`

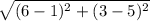
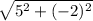
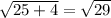
Since B and D are the points (6, 5) and (2, 2)

So length of BD =
`\sqrt{(6-2)^(2)+(5-2)^(2)}`

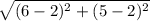
BD =
`\sqrt{4^(2)+3^(2)}=√(25)=5`

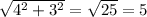
Now we will put these values in the formula

Area of parallelogram =
`(1)/(2)(√(29))(5)`

=
`(5)/(2)` ×
`√(29)`

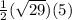
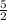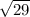
= (2.5) (5.385)

= 13.46