Question

Triangle CDE and triangle CFG are similar right triangles. Which proportion can be used to show that the slope of CE is equal to the slope of CG?

A) 2 − 3
2 − 0
= 3 − 1
4 −0

B) 3 − 2
2 − 0
= 3 − 1
4 − 0

C) 2 − 3
0 − 2
= 3 − 1
0 − 4

D) 3 − 2
0 − 2
= 3 − 1
0 − 4

Answer 1

The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

We have the points E(2, 2), C(0, 3) and G(4, 1), C(0, 3).

Substitute:

`(3-2)/(0-2)=(3-1)/(0-4)\to\boxed{D}`

Answer 2

Answer: The correct option is (D)
`(3-2)/(0-2)=(3-1)/(0-4).`

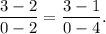
Step-by-step explanation: Given that ΔCDE and ΔCFG are similar right triangles.

We are to select the correct proportion that can be used to show that the slope of CE is equal to the slope of CG.

We know that the slope of a line passing through two points (a, b) and (c, d) is given by

`m=(d-b)/(c-a).`

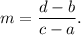
From the given figure, we note that the co-ordinates of the points C, E and G are

C(0, 3), E(2, 2) and G(4, 1).

So, the slope of line CE is given by

`m_1=(2-3)/(2-0),`

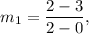
and the slope of line CG is given by

`m_2=(1-3)/(4-0).`

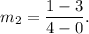
Since the lines CE and CG are same, they must be parallel and hence they have equal slopes.

Therefore,

`m_1=m_2\\\\\\\Rightarrow(2-3)/(2-0)=(1-3)/(4-0)\\\\\\\Rightarrow (3-2)/(0-2)=(3-1)/(0-4).`

Thus, (D) is the correct option.