Answer:
The length of arc is 185.39 m
Explanation:
Given that in a circle with a radius of 36.9 m, an arc is intercepted by a central angle of
 radians.
radians.
we have to find the arc length.
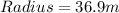
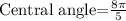
The arc length can be calculated by the formula

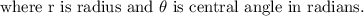
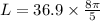
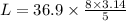
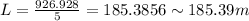
hence, the length of arc is 185.39 m