Line AB passes through points A(–6, 6) and B(12, 3). If the equation of the line is written in slope-intercept form, y = mx + b, then m = –1/6. and b = ?

Question

asked Apr 27, 2019 46.9k views

2 Answers

Rafael Kennedy · Answer 1 · 2019-04-29T07:55:22+0000

Answer:

The value of b is 5.

Explanation:

Consider the provided information.

It is given that the slope intercept form is, y = mx + b

Where m is the slope and b is the y intercept.

Also, it is given that the slope of the line is -1/6.

Line AB passes through points A(–6, 6) and B(12, 3).

That means Point A and B must satisfy the equation of line.

Substitute
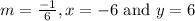$m=(-1)/(6), x=-6\ \text{and}\ y = 6$ in slope intercept form:

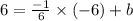
6=(-1)/(6)*(-6)+b

6=1+b

5=b

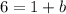
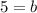
Thus, the value of b is 5.

Toolshed · Answer 2 · 2019-05-03T20:13:34+0000

Put the value of slope to the equation of the function:

y=-(1)/(6)x+b

Put the coordinates of the point B(12, 3) to the equation:

3=-(1)/(6)(12)+b

3=-2+b add 2 to both sides

5=b