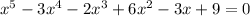
Fifth degree polynomial; scary stuff. We know it has five complex roots, counting multiplicities. How many are real?
The rational root test tells us we only have to try the divisors of 9, so 1, -1, 3, -3, 9, -9. We find x=3 gives
243 - 243 - 54 + 54 - 9 + 9 = 0
in nice pairs.
So x-3 is a factor and we can divide to get a 4th degree polynomial. The division is a bit easier than usual.
x^4 - 2x^2 - 3
x - 3 | x^5 - 3x^4 - 2x^3 + 6x^2 - 3x + 9
x^5 - 3x^4
0 - 2x^3 + 6x^2
0 - 3x + 9
0
So we get

It's downhill from here. The new factor is really just a quadratic in x squared, and factors easily:
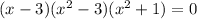
And now if we descend into irrational and complex numbers, we can further factor
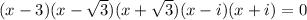
and we can read off our roots,

We have one rational root, namely 3, and two irrational roots, the square roots of three, and two purely imaginary roots.
Answer: 1 rational, 2 irrational