Question

What is the area of a rectangle with vertices at (1, 7) , (5, 3) , (3, 1) , and (−1, 5) ?

PLEASE HELPPPPPPP

and explain

Answer 1

Given the vertices of the rectangle ABCD:

A = (1, 7) , B = (5, 3), C = (3,1) and D = (-1, 5)

Distance(D) formula for two points is given by;

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

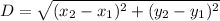
Using distance formula:

`AB = √((5-1)^2+(3-7)^2)=√((4)^2+(-4)^2) = √(16+16) = √(32) = 4√(2)` units

`BC= √((3-5)^2+(1-3)^2)=√((-2)^2+(-2)^2) = √(4+4) = √(8) = 2√(2)` units.

`CD = √((-1-3)^2+(5-1)^2)=√((-4)^2+(4)^2) = √(16+16) = √(32) = 4√(2)` units

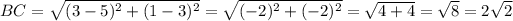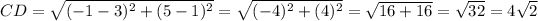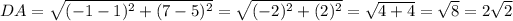`DA= √((-1-1)^2+(7-5)^2)=√((-2)^2+(2)^2) = √(4+4) = √(8) = 2√(2)` units.

Since, the Opposite sides of a rectangle are the same length.

⇒AB = CD and BC =DA

Area of rectangle is equal to multiply its width by length.

Area of rectangle ABCD =
`CD * BC`

=
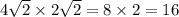`4√(2) * 2√(2) = 8 * 2 = 16` square units.

Therefore, the area of rectangle is, 16 square units.