Question

The pair of numbers (x; y), which is NOT a solution of the equation x2 - 2x + y2 = 1, is

Answer 1

the pair of numbers (x; y), which is NOT a solution of the equation
`x^(2) -2x+y^(2) =1` is that point whose distance from the point (1,0) is greater or less than
`√(2)`.

Explanation:

Given: The equation is
`x^(2) -2x+y^(2) =1`.

To find: The pair of numbers (x; y), which is NOT a solution of the equation
`x^(2) -2x+y^(2) =1`.

We have
`x^(2) -2x+y^(2) =1`.

⇒
`x^(2) -2x+1+y^(2) =1+1`

⇒
`(x-1)^2+y^2=2`

⇒
`(x-1)^2+(y-0)^2=√(2)`

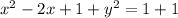
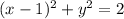
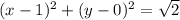
This is an equation of circle with centre at (1,0) and radius
`√(2)`.

So, only those pair of numbers will satisfy the equation whose distance from the point (1,0) is
`√(2)`.

Hence, the pair of numbers (x; y), which is NOT a solution of the equation
`x^(2) -2x+y^(2) =1` is that point whose distance from the point (1,0) is greater or less than
`√(2)`.