Answer:
Number of units of first product = 112
Number of units of second product = 400
Explanation:
Given that there are two products which are to be shipped.
First product details:
Unit volume = 10 cu ft
Weight of one unit = 50 lb
Second product details:
Unit volume = 3 cu ft
Weight of one unit = 40 lb
Total volume that can be carried by a truck = 2320 cu ft
Total weight that can be carried by a truck = 21600 cu ft
To find:
The number of units of each product that can be transported in one shipment in the truck?
Solution:
Let number of units of first product =

Let number of units of second product =

We can write down two linear equations in two variables here and solving them will give us the answer we are required to find.
As per question statement, the equations can be written as:
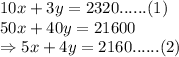
Multiplying equation (2) with 2 and subtracting equation (1) from it:
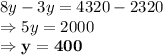
By equation (1):
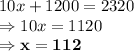
Answer is:
Number of units of first product = 112
Number of units of second product = 400