Question

Prove the triangle proportionality Theorem.

Answer 1

Statement of triangle proportionality:

If a line parallel to one side of a triangle intersects the other two sides of the triangle, then that line divides these two sides proportionally.

From the statement: If
`FG || BC` then,

Show that:
`(FB)/(FA) = (GC)/(AG)`

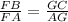
Consider
`\triangle ABC` and
`\triangle GFA`

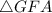
Reflexive property states that the value is equal to itself.

`\angle BAC \cong \angle GAF` [Angle] {Reflexive property of equality}

Corresponding angles theorem states that if the two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent(i., e equal).

`\angle ABC \cong \angle GFA` [Angle]

`\angle ACB \cong \angle AGF` [Angle]

AA Similarity states that the two triangles have their corresponding angles equal if and only if their corresponding sides are proportional.

then, by AA similarity theorem:

`\triangle ABC \sim \triangle GFA`

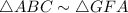
By segment addition postulates:

AB = FA +FB and AC = AG + GC

Corresponding sides in similar triangles are proportional

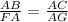`(AB)/(FA) = (AC)/(AG)` .....[1]

Substitute AB = FA +FB and AC = AG + GC in [1]

we have;

`(FA+FB)/(FA) = (AG+GC)/(AG)`

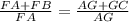
Separate the fraction:

`(FA)/(FA) + (FB)/(FA) = (AG)/(AG) + (GC)/(AG)`

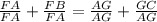
Simplify:

`1 + (FB)/(FA) =1+ (GC)/(AG)`

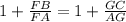
Subtract 1 from both sides we get;

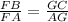`(FB)/(FA) =(GC)/(AG)` hence proved