Question

Hi any chance that somebody can help me with 9, 10, and 11? Thank u so much for your help if you know how!!! ❤️

Answer 1

✿ Heya! Grace ✿

✿ Nice Flower Drawing ✿

9. Given : The Length of the Side of the Square is
`\mathsf{: 48√(2)}`

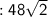
We know that : Area of a Square is given by : Side × Side

`\mathsf{\implies The\;Area\;of\;the\;Given\;Square = (48√(2)) * (48√(2))}`

`\mathsf{\implies The\;Area\;of\;the\;Given\;Square = (48√(2))^2}`

`\mathsf{\implies The\;Area\;of\;the\;Given\;Square = (48)^2(2)}`

`\mathsf{\implies The\;Area\;of\;the\;Given\;Square = (2304)(2)}`

`\mathsf{\implies The\;Area\;of\;the\;Given\;Square = 4608\;Inch^2}`

----------------------------------------------------

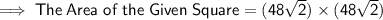
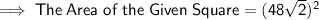
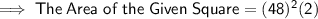
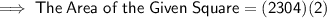
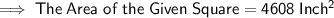
10. Given : The Length of Rectangular Prism
`\mathsf{= √(5)\;feet}`

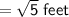
Given : The Width of Rectangular Prism
`\mathsf{= 2 + √(3)\;feet}`

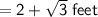
Given : The Height of Rectangular Prism
`\mathsf{= 2 - √(3)\;feet}`

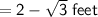
We know that : Volume of a Rectangular Prism is given By :

✿ Length × Width × Height

⇒ Volume of the Given Rectangular Prism is :

✿
`\mathsf{(√(5)) * (2 + √(3)) * (2 - √(3))}`

`\mathsf{\implies (√(5)) * (2^2 - (√(3))^2)}`

`\mathsf{\implies (√(5)) * (4 - 3)}`

`\mathsf{\implies √(5)}`

-------------------------------------------------------------

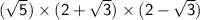
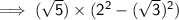
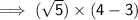
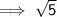
11. (a)

Given : The Length of First Leg
`\mathsf{= 3 + √(3)\;feet}`

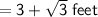
Given : The Length of Second Leg
`\mathsf{= 3 - √(3)\;feet}`

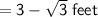
We know that, From Pythagorean Theorem :

✿ (Hypotenuse)² = (First Leg)² + (Second Leg)²

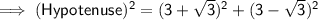
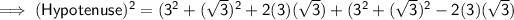
`\mathsf{\implies (Hypotenuse)^2 = (3 + √(3))^2 + (3 - √(3))^2}`

`\mathsf{\implies (Hypotenuse)^2 = (3^2 + (√(3))^2 + 2(3)(√(3)) + (3^2 + (√(3))^2 - 2(3)(√(3))}`

`\mathsf{\implies (Hypotenuse)^2 = [3^2 + (√(3))^2] + [3^2 + (√(3))^2]}`

`\mathsf{\implies (Hypotenuse)^2 = (2) [3^2 + (√(3))^2]}`

`\mathsf{\implies (Hypotenuse)^2 = (2) [9 + 3]}`

`\mathsf{\implies (Hypotenuse)^2 = (2)(12)}`

`\mathsf{\implies (Hypotenuse)^2 = 24}`

`\mathsf{\implies Hypotenuse = √(24)}`

`\mathsf{\implies Hypotenuse = 2√(6)}`

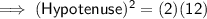
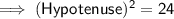
(b). We know that Perimeter of a Triangle is given by Adding the Lengths of all the Three Sides of the Triangle.

`\mathsf{\implies Perimeter\;of\;the\;Given\;Triangle = [(3 + √(3)) + (3 - √(3)) + 2√(6)]}`

`\mathsf{\implies Perimeter\;of\;the\;Given\;Triangle = [(3 + 3 + 2√(6)]}`

`\mathsf{\implies Perimeter\;of\;the\;Given\;Triangle = (6 + 2√(6))\;feet}`

(c). We know that : Area of a Triangle is given by :

✿
`\mathsf{(1)/(2) * Base * Height}`

`\mathsf{\implies Area\;of\;Given\;Triangle = (1)/(2)(3 + √(3))(3 - √(3))}`

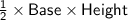
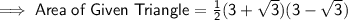
`\mathsf{\implies Area\;of\;Given\;Triangle = (1)/(2)[3^2 - (√(3))^2]}`

`\mathsf{\implies Area\;of\;Given\;Triangle = (1)/(2)[9 - 3]}`

`\mathsf{\implies Area\;of\;Given\;Triangle = (1)/(2)(6)}`

`\mathsf{\implies Area\;of\;Given\;Triangle = 3\;feet^2}`