Question

Social Science predicts that the population of barre, Vermont will double every 54 years. If the population in 1974 was 56000, in what year should we expect the population to reach 71000

Answer 1

We should expect the population to reach 71000 in 1993.

Explanation:

If the population will double every 54 years and the population in 1974 was 56000 people, then the function that represents this situation is

`y=56000\cdot 2^{(x)/(54)},`

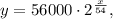
where x is time in years since 1974.

Nota that in 1974, x=0, then y=56000 and after 54 years the population will be
`y=56000\cdot 2^{(54)/(54)}=56000\cdot 2=112000.`

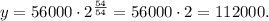
Therefore, you have to calculate x, when y=71000:

`71000=56000\cdot 2^{(x)/(54)},\\ \\(71)/(56)=2^{(x)/(54)},\\ \\(x)/(54)=\log_2(71)/(56),\\ \\x=54\log_2(71)/(56)\approx 18.49`

Thus, we should expect the population to reach 71000 in 1993 (after full 19 years).