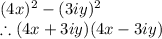Answer:
1.
When we are completing squares, we need to divide by 2 the linear term and then find its square power, that's the term we need to add on both sides of the equality, as follows
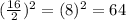
Basically, we need to add the number 64 both sides

2.
The given equation is
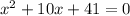
We need to apply the quadratic formula to solve this equation
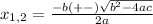
Where
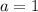 ,
,
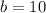 and
and
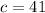 . Replacing these values, we have
. Replacing these values, we have
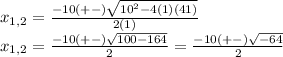
There we need to use complex number, to transform the subradical number in a positive number
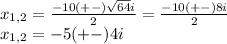
Therefore, the complex solutions are
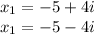
3.
The given expression is
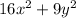
To solve this expression, remember that
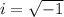
First, we expresse both squares uniformly,

But, we know that
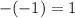 , so
, so
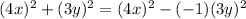
Then,
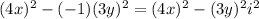 , because
, because
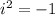
Therefore, the expression with complex numbers is