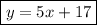Question

Write the equation of a line that is perpendicular to the given line and that passes through the given point.

y-3=-1/5(x+2);(-2,7)

Answer 1

The point-slope form:

`y-y_1=m(x-x_1)`

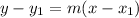
m - slope

We have the line

`y-3=-(1)/(5)(x+2)\to m=-(1)/(5)`

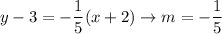
If m₁ and m₂ are the slopes of the perpendicular lines, then

`m_1m_2=-1\to m_2=-(1)/(m_1)`

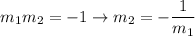
Therefore the slope of ouer line is

`m=-(1)/(-(1)/(5))=5`

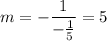
We have the point (-2, 7). Put the coordinates to the equation of a line in the point-slope form:

`y-7=5(x-(-2))`

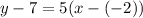
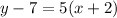`y-7=5(x+2)` use the distributive property

`y-7=(5)(x)+(5)(2)`

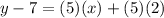
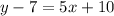`y-7=5x+10` add 7 to both sides

`\boxed{y=5x+17}`