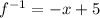Question

What is the domain and range for the following function and its inverse? f(x) = -x + 5

Answer 1

The domain of linear function is always the set of all real numbers

Range is also the set of all real numbers

`f^(-1)=-x+5`

Explanation:

`f(x) = -x + 5`

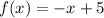
Domain is the set of x value and range is the set of y value. There is no restriction for x and y in a linear function.

The domain of linear function is always the set of all real numbers

Range is also the set of all real numbers

Now find the inverse

`f(x) = -x + 5`

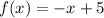
Replace f(x) with y

`y = -x + 5`

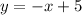
Replace x with y and y with x

`x = -y + 5`

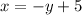
Subtract 5 from both sides

`x-5=-y`

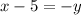
Divide both sides by -1

`y=-x+5`

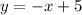
Replace y by f^-1

`f^(-1)=-x+5`

Answer 2

Domain:
`\mathbb{R}`

Inverse:
`f^(-1)(x) = -x + 5`

Explanation:

Since this is a linear function, the domain and range is simply the set of real numbers.

The inverse is obtain by switching the places of x and y, then solving for y.

Here,

y = -x + 5

So switching x and y,

x = -y + 5

Solving for y again,

y = -x + 5

Thus,

`f^(-1)(x) = -x + 5`