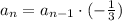Answer:
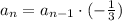
Explanation:
The explicit formula for the geometric sequence is given by:
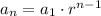
where,
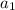 is the first term
is the first term
r is the common ratio to the following terms.
As per the statement:
Given the explicit formula for geometric sequence:

On comparing with [1] we have;
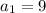 and
and
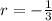
The recursive formula for geometric sequence is given by:

Substitute the given values we have;
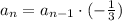
Therefore, the recursive formula for the geometric sequence is,