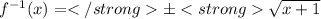Question

If f(x) = x2 -1, what is the equation for f–1(x)?

Answer 1

Inverse function is

`f^(-1)(x)=\pm √(x+1)`

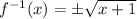
Explanation:

Given that
`f(x)=x^2-1`

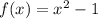
Now using that equation of f(x), we need to find equation of the inverse function

`f(x)=x^2-1`

`f^(-1)(x)`

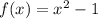
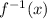
Step 1: Replace
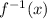`f^(-1)(x)` with y

`y=x^2-1`

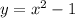
Step 2: Switchx and y

`x=y^2-1`

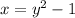
Step 3: Solve for y

`x=y^2-1`

`x+1=y^2-1+1`

`x+1=y^2`

`y^2=x+1`

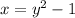
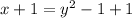
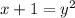
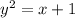
take square root of both sides

`y=\pm √(x+1)`

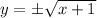
Hence inverse function is

`f^(-1)(x)=</strong>\pm <strong>√(x+1)`

Answer 2

`f^(-1)=+-√(x+1)`

Explanation:

f(x) = x^2 -1

We need to find f^-1(x)

WE find inverse of f(x)

Replace f(x) with y

`y= x^2 -1`

Replace x with y and y with x

`x= y^2 -1`

Solve for y

add 1 on both sides ,
`x+1= y^2`

To remove square , take square root on both sides

`√(x+1) =√(y^2)`

`√(x+1) =y`

`y=+-√(x+1)`

Replace y with f^-1

`f^(-1)=+-√(x+1)`