Question

How many solutions does the system of equations have ? Y= 6x +2 and 3y-18x=12

Answer 1

0 solutions

Explanation:

same slope, different y intercepts so they never intersect

Answer 2

As both slopes are equal, and the values of b are different it means that the two lines are parallel and the system of equations does not have any solution. (Please see the picture below)

Explanation:

1. First write the system of equations:

`y=6x+2`

`3y-18x=12`

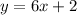
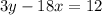
2. Solve y for the second equation:

`3y-18x=12`

`3y=18x+12`

`y=(18x+12)/(3)`

`y=6x+4`

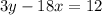
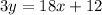
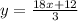
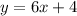
3. Re write both equations in the form y=mx+b, where m is the slope and b is the value of y when x=0 :

`y=6x+2`

`y=6x+4`

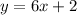
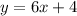
As both slopes are equal, and the values of b are different it means that the two lines are parallel and the system of equations does not have any solution.