Question

Suppose A and B represent two different school populations where A > B and A and B must be greater than 0. Which of the following expressions is the largest? Explain why. Show all work necessary. 2(A + B) (A + B)2 A2 + B2 A2 − B2

Answer 1

Answer: (A+B)^2 is the largest because it equals 9 when A=2 and B=1 are plugged in and the rest are less than 9

Answer 2

The value for the expression
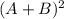`(A+B)^(2)` is the largest

Explanation:

Since both A and B must be greater than 0 and A>B then we can assume the least possible values for B=1 and A=2.

So,

i) 2(A+B) = 2(2+1) = 2*3 = 6

ii)
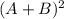`(A+B)^(2)` = (A+B)*(A+B) = (2+1)*(2+1) = 3*3 = 9

iii)
`A^(2) + B^(2)` =
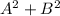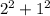`2^(2) +1^(2)` = 4+1 = 5

iv)
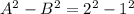`A^(2) - B^(2) = 2^(2) - 1^(2)` = 4-1 =3

Inspecting the answers of the above four expressions, we see that the value for the expression
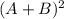`(A+B)^(2)` is the largest.