Given:
A line passes through two points (7, 9) and (2, −9).
To find:
The slope intercept form of the line.
Solution:
A line passes through two points (7, 9) and (2, −9), so the equation of line is
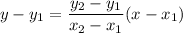
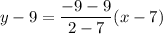
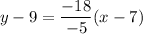
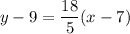
Using distributive property, we get
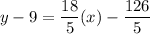
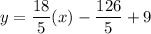

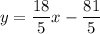
Therefore, the slope intercept form of the line is
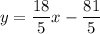 .
.