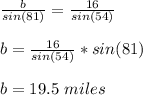Answer:
19.5 miles
Explanation:
The question is represented in the image attached.
∠A = 45°, ∠B = 45° + (216° - 180°) = 81°
∠A + ∠B + ∠C = 180° (sum of angles in a triangle)
45° + 81° + ∠C = 180°
126 + ∠C = 180
∠C = 180 - 126
∠C = 54°
The sine rule states that for a triangle with sides a, b, c and their corresponding opposite angles A, B and C. The following rule holds:

b = length of beginning of submarine to end point. Using sine rule: