Question

3. To combine the equations and solve for one of the variables, you need to eliminate the other variable. How can you change one equation so that one variable is eliminated when the two equations are added? Explain and write the new equation. 12x + 6y = 120

4x + y = 30
Combine the two equations to eliminate one of the variables, and then solve for the other.
Solve for the other variable.
Prove that your solutions are correct by substituting the values back into the original equations and verifying the answers.

Answer 1

x=5

y=10

Explanation:

Answer 2

12x + 6y = 120 -----(eq. 1)
4x + y = 30 -----(eq. 2)
4x + y = 30
4x = 30 - y
x = (30 - y)/4
Substituting this value of x in eq. 1, we get,


`12( (30 \: - \: y)/(4) ) \: + \: 6y \: = \: 120`

`3(30 \: - \: y) \: + \: 6y \: = 120`

`90 \: - \: 3y \: + \: 6y \: = \: 120`

`3y \: = \: 30`

`y \: = \: 10`

`x \: = \: (30 \: - \: y)/(4)`

`x \: = \: (30 \: - \: 10)/(4)`

`x \: = \: (20)/(4)`

`x \: = \: 5`
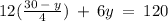
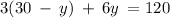
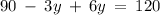
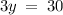
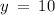
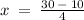
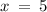
Hence, x = 5, and y = 10.
To verify, substitute the values in the equation,
4(5) + (10) = 30
30=30
12(5) + 6(10) = 120
120=120.