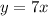Answer:
Option C is correct
Explanation:
Direct variation states that:
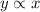 ......[1]
......[1]
then, the equation is in the form of:
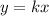 , where k is the constant of variation
, where k is the constant of variation
From the given graph we have points in the form of (x, y) i.e,
(0, 0), (5, 35), (10, 70), (15, 105), (20, 140), (25, 175) and (30, 210)
Substitute any points i.e (5, 35) in [1] we have;
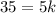
Divide both sides by 5 we have;
7 = k
or
k = 7
then;
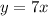
Therefore, the constant of proportionality for the graph is, 7 and its form is,