Question

A 10 meter long ladder rests against a vertical wall so that the distance between the foot of the ladder and the wall is 2 meter. Find the angle the ladder makes with the wall and height above the ground at which the upper end of the ladder touches the wall. Round your answer to the nearest hundredth of a degree if necessary.

Answer 1

ANSWER

The angle can be calculated using ,


`\sin(\ A) = (2)/(10)`



`\sin(\ A) = (1)/(5)`



`A= arcsin((1)/(5))`



`A=11.54\degree`



Using the tangent ratio,


`\tan(A) = (2)/( |AC| )`

This implies that,



`\tan(11.537) = (2)/( |AC| )`




`0.20412= (2)/( |AC| )`



`|AC| = (2)/( 0.20412 )`



`|AC| = 9.80m`

Answer 2

1. The angle ladder makes with the wall is 11.54°

2. The height above the ground at which the upper end of the ladder touches the wall is 9.80 m

Explanation:

• ∠A is what we are trying to find.
• Also AC is the length we are trying to find, as well.

We see that the side opposite of ∠A and the hypotenuse (side opposite of 90 degree angle) of the triangle are known. The ratio that relates these two sides are SINE.

We know,

`sin(angle)=(opposite)/(hypotenuse)`

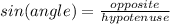
Thus we can write:

`sin(A)=(2)/(10)\\sin(A)=(1)/(5)`

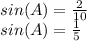
To find ∠A, we take the inverse sine of
`(1)/(5)`. Our answer is:

`sin(A)=(1)/(5)\\A=sin^(-1)((1)/(5))\\A=11.54`

Thus the angle ladder makes with the wall is 11.54°

Second part of the question asks for the height above the ground at which the upper end of the ladder touches the wall, this is the length of AC.

Given the angle we found, we see that the side AC is adjacent of the angle and we also know the hypotenuse. The ratio that relates these 2 sides is COSINE.

We know,

`cos(angle)=(adjacent)/(hypotenuse)`

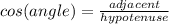
Thus, we can write:

`cos(11.54)=(AC)/(10)`

Cross multiplying and solving for AC, gives us:

`cos(11.54)=(AC)/(10)\\AC=10*cos(11.54)\\A=9.80`

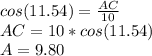
Thus, the height above the ground at which the upper end of the ladder touches the wall is 9.80 m