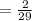ANSWER

Step-by-step explanation
Let the number who plays both games be

Then those who play only basketball
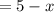
and those who play only baseball
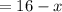
We were given that 10 students play neither sports.
We can then write the following equation,
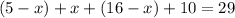
This implies that,
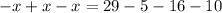
This simplifies to,
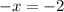
This gives us,
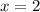
Therefore the number of students play both basketball and baseball is 2.
The probability that a student chosen from the class plays both basketball and baseball ball