Answer:
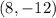
Explanation:
The two equations are:
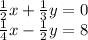
We can solve the first equation for
 and then substitute into second equation to find the value of
and then substitute into second equation to find the value of
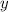 .
.
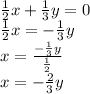
Now,
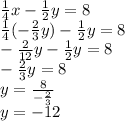
Substituting
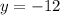 into the "solved for
into the "solved for
 " version of first equation, we get the value of
" version of first equation, we get the value of
 . So,
. So,
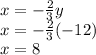
Hence the ordered pair is
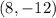 and this is the solution to the system of equations shown.
and this is the solution to the system of equations shown.