Answer:
Sequence 1 is an 'Arithmetic but not Geometric Sequence'
Sequence 2 is 'Geometric but not Arithmetic Sequence'
Explanation:
We know that,
1. Arithmetic Sequence is a sequence in which the difference of one term and the next term is a same constant for all terms.
2. Geometric Sequence is a sequence in which the division of two terms gives the same value for all terms.
Now, we check the above properties in the given options,
In Sequence 1 i.e.
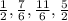 , . . . .
, . . . .
We see that the difference between the terms comes out to be
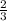 ,
,
for eg.
 =
=
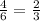
But, the division of two terms gives different values,
for eg.
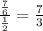 and
and
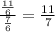
Hence, this sequence is not a Geometric Sequence but an Arithmetic Sequence.
In Sequence 2 i.e.
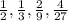 , . . . .
, . . . .
We see that the difference of terms is not same constant but are different values,
for eg.
 =
=
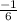 and
and
 =
=
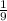
But, the division of different terms gives same constant i.e.
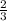 ,
,
for eg.
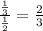 .
.
Hence, this sequence is not a Arithmetic Sequence but a Geometric Sequence.