Question

Which expression is equivalent to the following complex fraction? X+5/x+2-x+1/x^2+2x

Answer 1

Final answer will be the choice which matches best with expression

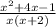`(x^2+4x-1)/(x\left(x+2\right))` or

`(x^2+4x-1)/(x^2+2x)`

Explanation:

Given expression is:

`(\left(x+5\right))/(\left(x+2\right))-(\left(x+1\right))/(\left(x^2+2x\right))`

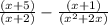
We begin by factoring denominators:

`=(\left(x+5\right))/(\left(x+2\right))-(\left(x+1\right))/(x\left(x+2\right))`

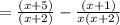
Multiply and divide first term by (x) to make denominators equal.

`=(x\left(x+5\right))/(x\left(x+2\right))-(\left(x+1\right))/(x\left(x+2\right))`

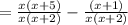
Since denominators are equal so we can combine numerators.

`=(x\left(x+5\right)-\left(x+1\right))/(x\left(x+2\right))`

Now simplify

`=(x^2+5x-x-1)/(x\left(x+2\right))`

`=(x^2+4x-1)/(x\left(x+2\right))`

`=(x^2+4x-1)/(x^2+2x)`

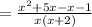
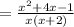
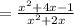
Hence final answer will be the choice which matches best with expression

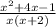`(x^2+4x-1)/(x\left(x+2\right))` or

`(x^2+4x-1)/(x^2+2x)`