Question

The coordinates of the point TT are (5,-6)(5,−6) and the coordinates of point UU are (-7,-6).(−7,−6). What is the distance, in units, between the point TT and point U?U?

Answer 1

The distance between points T and U is 12 units.

Explanation:

Let
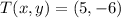`T(x,y) = (5,-6)` and
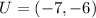`U = (-7,-6)`. The distance between points T and U represents a straight line, whose is length (
`TU`) can be determined by Pythagorean Theorem. That is:

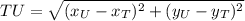`TU = \sqrt{(x_(U)-x_(T))^(2)+(y_(U)-y_(T))^(2)}` (1)

If we know that
`x_(T) = 5`,
`x_(U) = -7`,
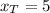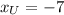`y_(T) = -6` and
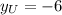`y_(U) = -6`, then the length between those coordinates is:

`TU = \sqrt{(-7-5)^(2)+[-6-(-6)]^(2)}`

`TU = 12`

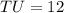
The distance between points T and U is 12 units.