Answer:
87 people in the restaurant, 45 people eat in the car and 57 people eat at home.
Explanation:
Let x be 'restaurant-purchased meals eaten in a restaurant', y be the 'restaurant-purchased meals eaten in a car' and z be the 'restaurant-purchased meals eaten at home'.
We can use the given information "the total number of restaurant-purchased meals that the average person will eat in a restaurant, in a car, or at home in a year is 189" to write an equation
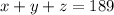 .
.
We can use the information "the total number of these meals eaten in a car or at home exceeds the number eaten in a restaurant by 15" to write another equation
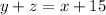 .
.
We can use the information "thirty more restaurant-purchased meals will be eaten in a restaurant than at home" to write the third equation as x=z+30
Now we need to solve this system of three equations to get the values of x, y and z.
We can solve for x directly from the first two equations.
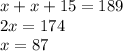
Substituting this value of x in the third equation we can get the value of z.

Finally, we can substitute the values of x and z in the first (or second) equation to get the value of y.
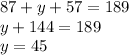
Therefore, 87 people in the restaurant, 45 people eat in the car and 57 people eat at home.