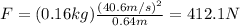Answer:
412.1 N
Step-by-step explanation:
First of all let's calculate the total speed of the ball as it is released, which is equal to the speed of the ball + the speed of the bowler:
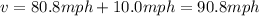
Now let's convert it into m/s. We know that
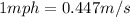
So
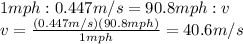
And now we can calculate the centripetal force, which is given by:
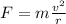
where
m = 0.16 kg is the mass of the ball
v = 40.6 m/s is the speed of the ball
r = 0.64 m is the radius of the circular path (equal to the length of the bowler's arm)
Substituting: