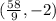Question

Point C(3.6, -0.4) divides in the ratio 3 : 2. If the coordinates of A are (-6, 5), the coordinates of point B are .

A (5,-4)
B (5,-2)
C (10,-4)
D (10,-2)

If point D divides in the ratio 4 : 5, the coordinates of point D are .
A (62/9,-4)
B (58/9,-4)
C (62/9,-2)
D (58/9,-2)

Answer 1

QUESTION 1

The point C(3.6, -0.4) divides AB in the ratio 3 : 2.

The coordinates of A are (-6, 5).

Let the coordinates of B be
`(x_2,y_2)`

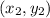
We use the formula:

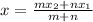`x=(mx_2+nx_1)/(m+n)` to determine the x-coordinate of B.

We substitute the known values to obtain:

`3.6=(3x_2+2(-6))/(3+2)`

`3.6=(3x_2-12))/(5)`

`3.6* 5=3x_2-12`

`18=3x_2-12`

`18+12=3x_2`

`30=3x_2`

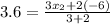
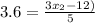
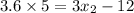
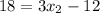
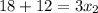
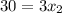
This implies that:

`x_2=10`

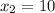
We also use the formula:

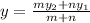`y=(my_2+ny_1)/(m+n)` to find the y-coordinate.

`-0.4=(3y_2+2(5))/(3+2)`

`-0.4=(3y_2+10)/(5)`

`-0.4* 5=3y_2+10`

`-2-10=3y_2`

`-12=3y_2`

`-4=y_2`

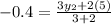
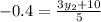
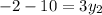
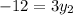
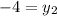
The coordinates of B are (10,-4)

QUESTION 2.

If point D divides CD in the ratio 4 : 5.

Then the coordinates of D are:

`((4(10)+5(3.6))/(4+5), (4(-4)+5(-0.4))/(4+5))`

`((58)/(9), (-18)/(9))`

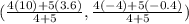
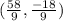
The coordinates of D are
`((58)/(9), -2)`