Question

An observer on top of a 50-foot tall lighthouse sees a boat at a 7° angle of depression. To the nearest foot, how far is the boat from the base of the lighthouse?

Answer 1

407.22 foot is the boat from the base of the lighthouse

Explanation:

Given the statement: An observer on top of a 50-foot tall lighthouse sees a boat at a 7° angle of depression.

Let x foot be the distance of the object(boat) from the base of the lighthouse

Angle of depression =
`7^(\circ)`

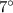
`\angle CAB = \angle DCA = 7^(\circ)` [Alternate angle]

In triangle CAB:

To find AB = x foot.

Using tangent ratio:

`\tan (\theta) = (Opposite side)/(Adjacent Base)`

`\tan (\angle CAB) = (BC)/(AB)`

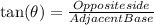
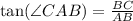
Here, BC = 50 foot and
`\angle CAB =7^(\circ)`

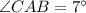
then;

`\tan (7^(\circ)) = (50)/(x)`

or

`x = (50)/(\tan 7^(\circ))`

`x = (50)/(0.1227845609)`

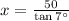
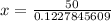
Simplify:

AB = x = 407.217321 foot

Therefore, the boat from the base of the light house is, 407.22'