QUESTION 1
The given ratio is
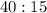
Let us write the ratio in terms of prime factors to obtain,
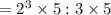
We cancel out the common factor of
5 to get

We simplify to get,
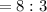
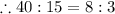
QUESTION 2
The given ratio is
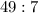
We factor each term in the ratio, it will now be
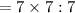
If we cancel out the common factor of 7, the ratio will now be
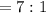
QUESTION 3
We want to simplify 80 inches over 10 days, which is,

We convert this into ratio to get,
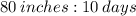
We factor the terms in the ratio to obtain,

We cancel out common factors to obtain,
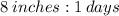
QUESTION 4
3 ounces costs $2.70.
We can write this as,
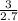
We change the denominator to fraction,
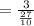
We change the first bar to a normal division sign to get,
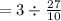
We now multiply by the reciprocal to get,
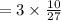
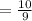
We convert this back to ratio to get,
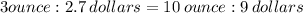
QUESTION 5
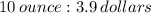
We multiply each term in the ratio by 10, to get,
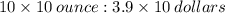
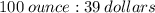
QUESTION 6
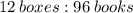
If we factor each term, the ratio
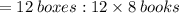
We cancel out the common factors and the ratio will be

QUESTION 7
The ratio of the sides of the triangle is
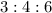
The total ratio is
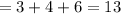
The shortest sides corresponds to the least ratio which is 3,
The shortest side is
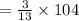
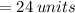
The length of the medium side is


The length of the longest side,
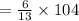
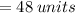
QUESTION 8.
The ratio of the sides of the triangle is
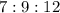
The total ratio is
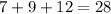
The shortest sides of the triangle corresponds to the least ratio which is 7,
The shortest side
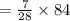
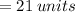
The length of the medium side is
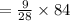
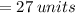
The length of the longest side is


QUESTION 9.
The given ratio is

The total ratio is

The length of the shortest side is,
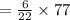
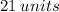
The length of the medium side is
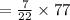
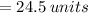
The length of the shortest side is
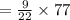
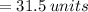
QUESTION 4
The given ratio is
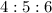
The total ratio is

The sum of the interior angles of the triangle is 180°.
The measure of the smallest angle is
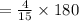

The measure of the medium angle is,
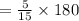
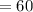
The measure of the biggest angle is

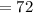
We could have also gotten this angle by subtracting the measure of the sum of smallest and the medium angle from 180°,
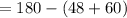
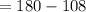
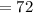
QUESTION 11
The given ratio is
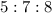
The sum of the total ratio is
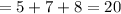
The measure of the biggest angle corresponds to the biggest ratio which is 8.
The biggest angle is
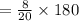
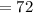
The measure of the smallest angle corresponds to 5,
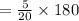
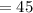
The measure of the third angle is

