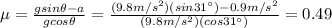Question

A block of mass 8.0 kg is held stationary on a slope whose surface is inclined 31 degrees relative to the horizontal.

When released it slides down the slope with a constant acceleration of 0.9 ms^-2.

Using your knowledge of forces, calculate the surface's coefficient of friction, μ. Assume g = 9.8 ms^-2.

Answer 1

0.49

Step-by-step explanation:

There are two forces acting on the block in the direction parallel to the surface of the inclined plane:

- The component of the weight of the block parallel to the incline:

`mg \sin \theta`

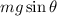
where m = 8.0 kg is the mass of the block, g=9.8 m/s^2 and
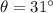`\theta=31^(\circ)` is the angle of the ramp

- The frictional force, given by:

`\mu mg cos \theta`

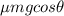
where
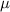`\mu` is the coefficient of friction.

The two forces act in opposite direction, and according to Newton's second law, their resultant is equal to the product of the mass of the block (m) and its acceleration (a):

`mg sin \theta - \mu mg cos \theta = ma`

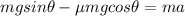
Since we knw that
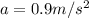`a=0.9 m/s^2`, we can re-arrange the equation to find the coefficient of friction:

`\mu = (g sin \theta -a)/( g cos \theta)=((9.8 m/s^2)(sin 31^(\circ))-0.9 m/s^2)/((9.8 m/s^2)(cos 31^(\circ)))=0.49`