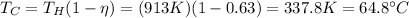Question

Assuming an engine operates as a reversible heat engine calculate the outlet temperature (temperature of rejected heat) that achieves a thermal efficiency of 63% if the engine takes in heat at 640°C .

Answer 1

`64.8^(\circ)C`

Step-by-step explanation:

The efficiency of a reversible heat engine is given by:

`\eta = 1 -(T_C)/(T_H)`

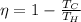
where

Tc is the cold temperature (outlet temperature)

Th is the hot temperature (temperature of the source)

In this problem, we know:

`\eta = 63\% = 0.63`

`T_H = 640^(\circ)C=913 K`

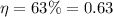
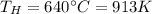
So, we can calculate the outlet temperature by re-arranging the formula:

`T_C = T_H ( 1 -\eta)=(913 K)(1- 0.63)=337.8 K=64.8^(\circ)C`