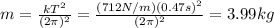Question

A horizontal spring oscillator consists of a mass attached to a spring of constant 712 N/m. There is no friction.

What mass (kg) should be attached for the oscillator to oscillate with a period of 0.47 seconds?

Answer 1

3.99 kg

Step-by-step explanation:

The period of a harmonic oscillator is given by:

`T=2 \pi \sqrt{(m)/(k)}`

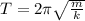
where

m is the mass attached to the spring

k is the spring constant

In this problem, we know:

k = 712 N/m

T = 0.47 s

Therefore, we can re-arrange the equation to find the mass that should be attached to the oscillator:

`m=(k T^2)/((2 \pi)^2)=((712 N/m)(0.47 s)^2)/((2 \pi)^2)=3.99 kg`