Question

Suppose a wheel with a tire mounted on it is rotating at the constant rate of 2.83 times a second. A tack is stuck in the tire at a distance of 0.393 m from the rotation axis. Noting that for every rotation the tack travels one circumference, find the tack's tangential speed

Answer 1

The tangential speed of the tack is 6.988 meters per second.

Step-by-step explanation:

The tangential speed experimented by the tack (
`v`), measured in meters per second, is equal to the product of the angular speed of the wheel (
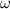`\omega`), measured in radians per second, and the distance of the tack respect to the rotation axis (
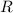`R`), measured in meters, length that coincides with the radius of the tire. First, we convert the angular speed of the wheel from revolutions per second to radians per second:

`\omega = 2.83\,(rev)/(s) * (2\pi\,rad)/(1\,rev)`

`\omega \approx 17.781\,(rad)/(s)`

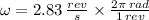
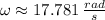
Then, the tangential speed of the tack is: (
`\omega \approx 17.781\,(rad)/(s)`,
`R = 0.393\,m`)

`v = \left(17.781\,(rad)/(s) \right)\cdot (0.393\,m)`

`v = 6.988\,(m)/(s)`

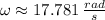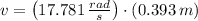
The tangential speed of the tack is 6.988 meters per second.