Question

If GF is a midsegment of CDE, find CD.

A. 3.4

B. 6.8

C. 13.6

D. 14

Answer 1

C. 13.6

Step-by-step explanation:

We have been given that GF is a mid-segment of CDE.

Since we know that mid-segment of a triangle is half the length of its parallel side.

We can see that ED is parallel to GF , so measure of GF will be half the measure of ED. We can represent this information as:

`GF=(1)/(2)ED`

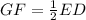
Let us substitute given value of GF and ED to find our x.

`2x+3=(1)/(2)(5x+4)`

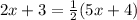
Multiply both sides of equation by 2.

`2*(2x+3)=2*(1)/(2)(5x+4)`

`2*(2x+3)=5x+4`

`4x+6=5x+4`

`6=5x+4-4x`

`6=x+4`

`6-4=x`

`2=x`

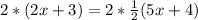
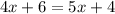
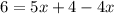
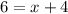
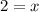
We can see that triangle CFG is similar to triangle CDE, so we will use proportions to find length of CD.

`(CF)/(GF)=(CD)/(ED)`

Substitute given values.

`(3x+0.8)/(2x+3)=(CD)/(5x+4)`

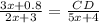
Upon substituting x=2 in our equation we will get,

`(3*2+0.8)/(2*2+3)=(CD)/(5*2+4)`

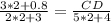
Let us simplify our equation.

`(6+0.8)/(4+3)=(CD)/(10+4)`

`(6.8)/(7)=(CD)/(14)`

`14*(6.8)/(7)=CD`

`2*6.8=CD`

`13.6=CD`

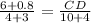
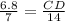
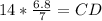
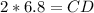
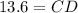
Therefore, CD equals 13.6 and option C is the correct choice.

Answer 2

C

Explanation:

Triangle CGF and triangle CED are similar. Hence, the ratio of their corresponding sides are equal. Thus we can write:

`(5x+4)/(2x+3)=(CD)/(3x+0.8)`

We can now cross multiply and solve for CD:

`(5x+4)/(2x+3)=(CD)/(3x+0.8)\\(5x+4)(3x+0.8)=(2x+3)(CD)\\15x^2+4x+12x+3.2=(2x+3)(CD)\\15x^2+16x+3.2=(2x+3)(CD)\\CD=(15x^2+16x+3.2)/(2x+3)`

Since GF is a midsegment of CDE, CD is double of CF. So we can write:

`CD=2CF\\(15x^2+16x+3.2)/(2x+3)=2(3x+0.8)\\(15x^2+16x+3.2)/(2x+3)=6x+1.6\\15x^2+16x+3.2=(6x+1.6)(2x+3)\\15x^2+16x+3.2=12x^2+18x+3.2x+4.8\\15x^2+16x+3.2=12x^2+21.2x+4.8\\3x^2-5.2x-1.6=0`

By using quadratic formula
`(-b+-√(b^2-4ac) )/(2a)` and with a=3, b= -5.2, and c= -1.6, we find the value of x to be:

`(5.2+-√((-5.2)^2-4(3)(-1.6)) )/(2(3))=2`

Since the expression for CD is
`(15x^2+16x+3.2)/(2x+3)` , we plug in
`x=2` into this expression to find value of CD:

`(15(2)^2+16(2)+3.2)/(2(2)+3)=13.6`

The correct answer is C