Question

What is the equation of the hyperbola with foci (0, 10), (0, ?10) and vertices (0, 6), (0, ?6)

Answer 1

y^2/36 - x^2/64 = 1

Hope this helps <3

Answer 2

As given,

Foci (0,10) ; (0,-10) and Vertices (0,6) ; (0,-6)

Now we know the general equation of hyperbola will be,

`(y^(2) )/(a^(2) ) -(x^(2) )/(b^(2) ) =1\\\\`

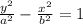
Now distance from origin to vertex is given, 6 ;

therefore,
`a=6`

And distance from origin to Focus is given ,
`c=10;\\`

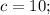
Using the equation,
`c^(2)=a^(2)+b^(2) \\c=10 ; a=6,`

Apply these values in the equation and find out the value of b,

`c^(2)=a^(2) +b^(2)\\10^(2)=6^(2)+b^(2)\\100=36+b^(2)\\100-36=b^(2)\\ b^(2)=64\\ b=8\\`

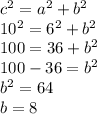
Hence equation of Hyperbola will be,

`(y^(2) )/(6^(2) )-(x^(2) )/(8^(2) )=1\\(y^(2) )/(36)-(x^(2) )/(64) =1`

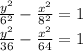
Here we are done.