Question

An ice cream cone that is 4cm across the top is topped with a single scoop of ice cream (spherical) that is 4cm in diameter. What is the minimum height of the cone so that when the ice cream melts, the ice cream does not overflow out of the cone? Justify your answer.

Answer 1

8 cm.

Explanation:

We have been given that an ice cream cone that is 4 cm across the top is topped with a single scoop of ice cream (spherical) that is 4 cm in diameter.

To find the minimum height of cone we will use volume of cone formula and volume of sphere as we are told that when the ice cream melts, the ice cream does not overflow out of the cone. This means that volume of sphere will be equal to volume of cone.

`\text{Volume of cone}=(1)/(3) \pi r^2h`

`\text{Volume of sphere}=(4)/(3) \pi r^3`

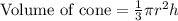
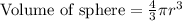
Since diameter of both cone and sphere is 4 cm, so radius will be half the diameter, that is 2 cm.

Let us substitute r=2 in both equations and equate the volumes of cone and sphere to find the height of cone.

`(4)/(3) \pi* 2^3=(1)/(3) \pi* 2^2* h`

`(4)/(3) \pi* 8=(1)/(3) \pi* 4* h`

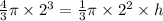
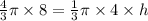
Multiply both sides of equation by 3.

`3* (4)/(3) \pi* 8=3* (1)/(3) \pi* 4* h`

`4 \pi* 8= \pi* 4* h`

`32 \pi= 4\pi* h`

`h=(32 \pi)/(4\pi)`

`h=8`

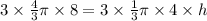
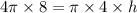
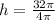
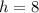
Therefore, the minimum height of cone must be 8 cm.